Interpreter Design Pattern

Interpreter design pattern gives the ability to define a language’s grammar with an interpreter, where in that interpreter uses that definition to interpret sentences of that language. I tried to rephrase and present it simpler in a line, what GoF has given for interpreter design pattern. I know the definition is kind of confusing. Let us decrypt it and understand the interpreter pattern in this tutorial.

Try to understand the following key points,

• Represent the grammar of a language.
• Use that definition in an interpreter to interpret a sentence.

Problem Area

This interpreter design pattern does not give solution for building a whole large interpreter for a language. It can be applicable for smaller chunks where grammar and interpretation is applicable. We can consider scenarios like regular expressions and interpreting mathematical expression.

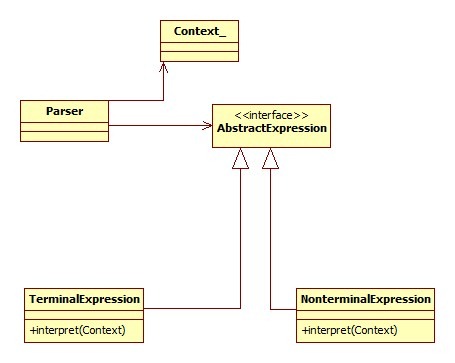
Interpreter Pattern Implementation

Let us quickly to move to an example and see hand in hand to understand the pattern. All we should do is

• create classes for each notations involved in the grammar
• each notation should be capable of interpreting itself.

• Let us construct an abstract tree for the expression (sentence) to be interpreted.
• TermialExpression – this will not contain other expression, the leaf node in a tree. Number in the following example.
• NonterminalExpression – this will contain other expression, non-leaf node in a tree. Operator in the following example.

Reverse Polish Notation (Postfix)

Mathematics is the most loved among all the sciences. Oops, who is that throwing stone at me? I felt that RPN is the simplest choice to explain this design pattern better and so chose it, so don’t curse me.

• Infix notation where the operator comes in between the operands. Example 1 + 2.
• In Polish notation (Prefix notation), the operator comes before the operand. Example + 1 2
• In reverse polish notation (postfix), the operator comes after the operand. Example 1 2 +

See, I told you Mathematics is lovable. ;-)

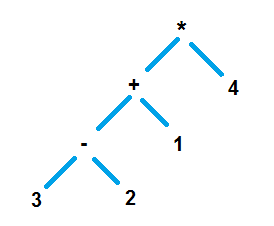
Following is the abstract tree for the expression (3 – 2 + 1) * 4

Interpreter Pattern Example

Let us consider a RPN and use interpreter design pattern to implement a solution to evaluate it.

Let us consider the expression 4 3 2 – 1 + *

Equivalent of this infix expression is, (3 – 2 + 1) * 4

There are already sooper-dooper algorithms available to covert postfix to infix and vice versa, so you can refer it straightly.

To implement an interpretation technique for this post-fix grammar let us use the interpreter design pattern. First let us define the elements. There are four different tokens present,

• numbers
• + operator
• – operator
• * operator

Let us define an interface contract which will have a method interpret(), so that we can enforce it on all the tokens. We should define classes for all these four tokens and these classes should implement the common interface. By implement it, all the four tokens themselves will know how to interpret.

package com.javapapers.designpatterns.interpreter;


public interface IExpression {
	public int interpret();
}

package com.javapapers.designpatterns.interpreter;

public class NumberExpression implements IExpression {
	int number;

	public NumberExpression(int i) {
		number = i;
	}

	public NumberExpression(String s) {
		number = Integer.parseInt(s);
	}

	@Override
	public int interpret() {
		return number;
	}

}

package com.javapapers.designpatterns.interpreter;

public class MultiplyExpression implements IExpression {

	IExpression leftExpression;
	IExpression rightExpresion;

	public MultiplyExpression(IExpression leftExpression,
			IExpression rightExpresion) {
		this.leftExpression = leftExpression;
		this.rightExpresion = rightExpresion;
	}

	@Override
	public int interpret() {

		return leftExpression.interpret() * rightExpresion.interpret();
	}

}

package com.javapapers.designpatterns.interpreter;

public class PlusExpression implements IExpression {
	IExpression leftExpression;
	IExpression rightExpresion;

	public PlusExpression(IExpression leftExpression, IExpression rightExpresion) {
		this.leftExpression = leftExpression;
		this.rightExpresion = rightExpresion;
	}

	@Override
	public int interpret() {
		return leftExpression.interpret() + rightExpresion.interpret();
	}

}

package com.javapapers.designpatterns.interpreter;

public class MinusExpression implements IExpression {

	IExpression leftExpression;
	IExpression rightExpresion;

	public MinusExpression(IExpression leftExpression,
			IExpression rightExpresion) {
		this.leftExpression = leftExpression;
		this.rightExpresion = rightExpresion;
	}

	@Override
	public int interpret() {

		return leftExpression.interpret() - rightExpresion.interpret();
	}

}

Interpretation Parser

Algorithm for postfix expression parser implementation is simpler than for infix.

1. Read token one by one and loop till end of expression
2. Is read element a number 
1. true then, push it to a stack
2. false then,
1. pop two elements from stack
2. apply the operator
3. push the result to stack

package com.javapapers.designpatterns.interpreter;

import java.util.Stack;

public class InterpreterPattern {
	public static void main(String args[]) {
		String tokenString = "4 3 2 - 1 + *";
		Stack stack = new Stack();

		String[] tokenList = tokenString.split(" ");
		for (String s : tokenList) {
			if (isOperator(s)) {
				IExpression rightExpression = stack.pop();
				IExpression leftExpression = stack.pop();
				IExpression operator = getOperatorInstance(s, leftExpression,
						rightExpression);
				int result = operator.interpret();
				stack.push(new NumberExpression(result));
			} else {
				IExpression i = new NumberExpression(s);
				stack.push(i);
			}
		}
		System.out.println("Result: "+stack.pop().interpret());
	}

	public static boolean isOperator(String s) {
		if (s.equals("+") || s.equals("-") || s.equals("*"))
			return true;
		else
			return false;
	}

	public static IExpression getOperatorInstance(String s, IExpression left,
			IExpression right) {
		switch (s) {
		case "+":
			return new PlusExpression(left, right);
		case "-":
			return new MinusExpression(left, right);
		case "*":
			return new MultiplyExpression(left, right);
		}
		return null;
	}
}